Lorenzo Bartolini, Stefano Bolognesi†  and Sven Bjarke  Gudnason

† : corresponding author

In this paper [1], we use a higher-dimensional model by Witten and Sakai–Sugimoto, which is a construction derived from string theory in 10 di- mensions, which at low energies gives an effective model in 5 dimensions that describes Quantum Chromodynamics (QCD), which is the theory gov- erning the strong forces that confine quarks into the proton and the neutron. The 5-dimensional theory is in a class of theories discovered in 1997 by Maldacena which is called holographic theo- ries and the framework is generally known as the AdS/CFT correspondence. A holographic theory is a theory with one dimension in addition to the 3 dimensions we can observe (and time) and the extra dimension is cleverly a pathway into probing the theory at higher energies.  Probing the theory at the other end and making sure that the theory is consistent in the bulk, allows one to read off physical quantities at low energies of a theory that is not perturbative. Per- turbation theory is a scheme that uses a series to determine the results order-by-order in a small coupling constant. This works very well for the theory of electrodynamics, but not for the strong force (QCD). Holography can give results for such strongly coupled theories and we use it to read off the electric dipole moment of the deuteron, which is an interesting physical quantity to calculate, since it has not yet been discovered. We know from experiments that it must be extremely small and the result we find in this paper is consistent with the experimental bounds. We find the number, corresponding to the electric dipole moment of the deuteron by integrating a solution to a partial differential equation in 5 dimensions, see Fig. 1, and the integral of the density in the figure is pro- portional to the result we find (the overall constant is simple to work out). This  number is yet to be discovered in experimental physics and probably will grant a Nobel  prize.

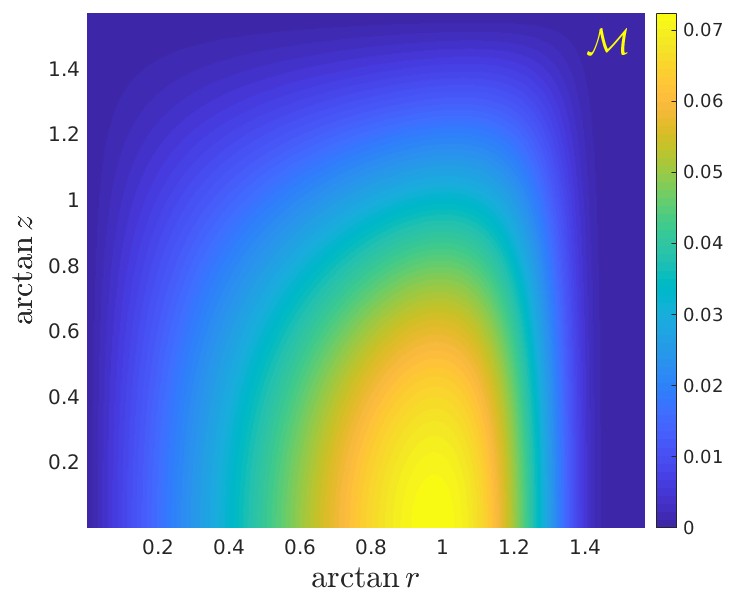
Figure  1: The  density  giving   rise to the electric dipole moment of the deuteron.

Publication

[1] L. Bartolini,  S.  Bolognesi  and  S.  B.  Gudnason,  “Deuteron  electric  dipole moment from holographic QCD,” Phys. Rev. D 101, no.8, 086009 (2020) doi:10.1103/PhysRevD.101.086009  [arXiv:1912.01641  [hep-th]].