Sven Bjarke Gudnason†  and Muneto  Nitta

† : corresponding author

In this paper [1], I prove a theorem that states that a Skyrmion in 3 dimensions must contain a link of two lines, which we can interpret as vortices. Witten has shown in 1983 that the Skyrmion is the baryon or the nucleon of QCD in the limit of a large number of quark colors, which is an approximation often used in theoretical physics. In the Skyrmion description of nuclei, there are no quarks left, but only topological structures in the pion fields. More generally, my result is that a nucleus with atomic number A has two vortex lines that are linked A times, see Fig. 1. The proof of the theorem utilizes a Hopf map and its inverse. The linking number may be a sum over clusters of simply linked parts. This result shows that Lord Kelvin in 1868 was not quite right, as he imagined that atoms were made of knots of vortices, but he was also not wrong. Interestingly, we can see from topological structure in Fig. 1(c) that the alpha particle (the nucleus of helium-4) is a bound state of two deuterium cores (fig. 1(b)).

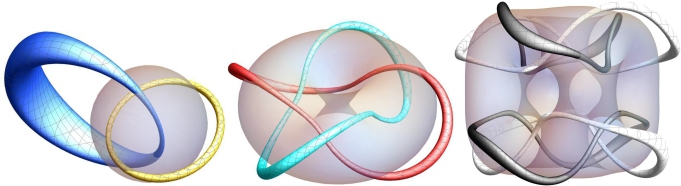
(a)                                           (b)                                           (c)

Figure 1: Vortex lines are linked once, twice and four times, respectively, for (a) the nucleon, (b) deuterium, and (c) helium-4. 

Publication

[1] S. B. Gudnason and M. Nitta, “Linking  number  of  vortices  as  baryon  num- ber,”  Phys.  Rev.  D  101,  no.6,  065011  (2020)   doi:10.1103/PhysRevD.101.065011

[arXiv:2002.01762  [hep-th]].